先日の自動車技術会学術講演春季大会(2023 年 5月)でリカレンスプロ ット(Recurrence Plot)が色々ご質問を受けたので解説文をアップすることにしました。
ーーー
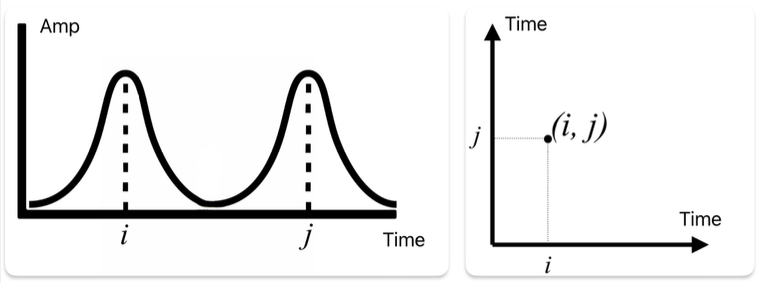
時系列の解析ではミクロ的な時間のトレンド(季節性)そしてマクロ的な時間のトレンド (年単位)を行う。 時間を経て同じような傾向が生まれる瞬間を周期性がある、相関があると判断。 そして、立体的な理解を行う手法としてリカレンスプロット(Recurrence Plot)があ る。
これは、時系列データ上同じ値のポイントを二次元で図示することで周期性を特徴ある模様として表現できる。
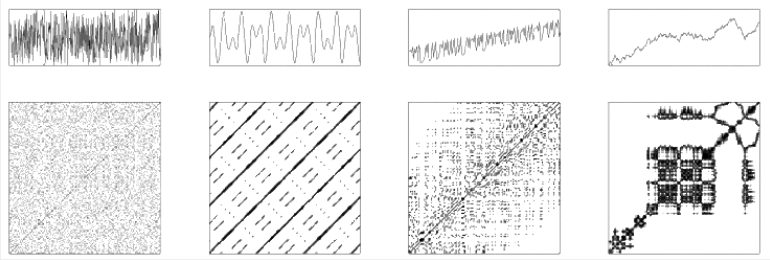
左より、ホワイトノイズ、倍音のある成分あるいは季節性のあるトレンド、トレンドがあるカオスデータ、自己回帰を持つプロット
参照:Wikipedia (https://en.wikipedia.org/wiki/Recurrence_plot)
さて、音の世界に応用する前に、再度ホワイトノイズと、サイン波を検証した。
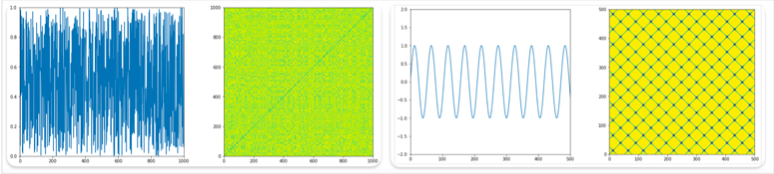
リカレンスプロットの性質から、その波形自身と同一になる二次関数での Y = X 直線がどのような波形でも刻印される。 ホワイトノイズの場合は、ランダムであるため、周期性のあるような模様は見られない。 一つの周波数で構成されるサイン波の場合は、同じ高さの波が繰り返し同じタイミング現 れるため格子状になる。
この二つの波形を混ぜ合わせると、格子がぼやけた波形にもなる。
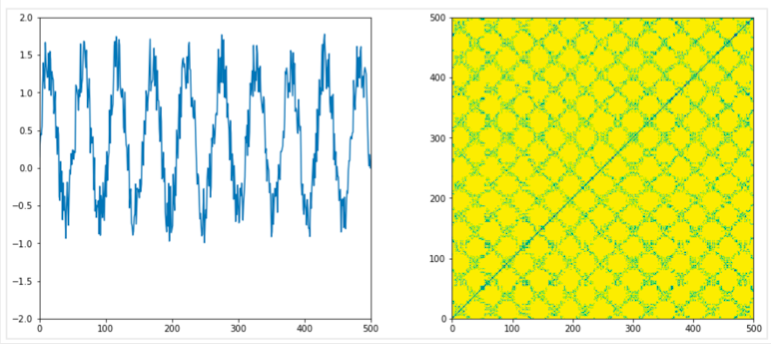
リカレンスプロットは倍音のような繰り返しのある波形分析に有利と思われ、サイン波の合成音、楽器の音でバイオリン、フルートを比較した。
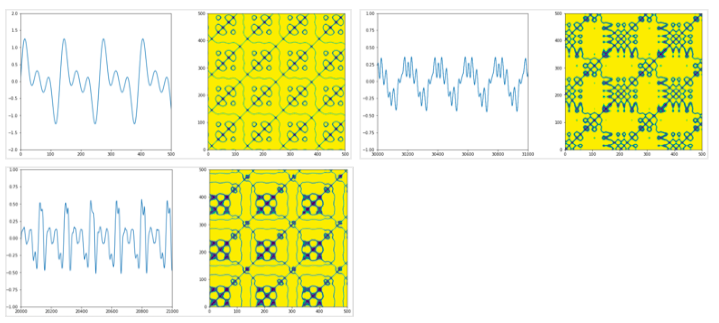
倍音を持つ音波形が描く模様に明らかな差異が見られた。
同様に倍音の多いエンジン音、アイドリング時の音を見てみた。
Lamborghini
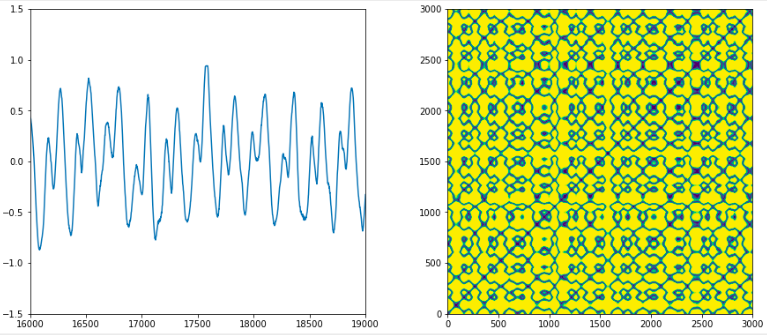
Ferrari 数車種
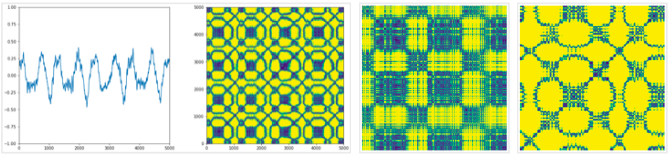
フェラーリはフラワー状になる傾向が他のフェラーリ車でも見られた。”フェラーリフラワ ー”と呼ぶことにした。そこで”フェラーリフラワー”を CNN で判定できるか検証した。
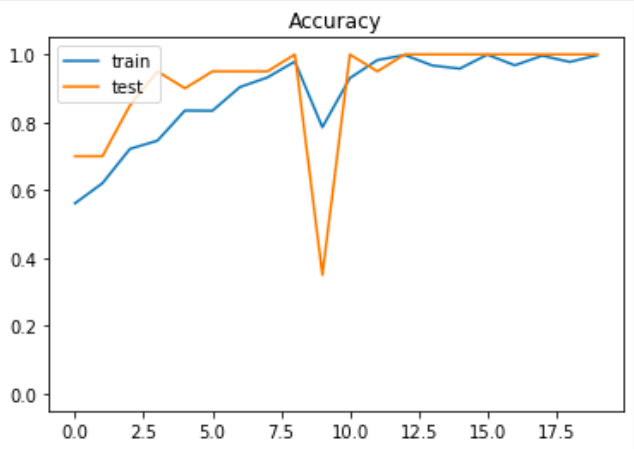
正答率 100 %にもなり、個別検証も良好だった。
